News
Recent Publications
M. Kahle, E. Paquette, É. Roldán
Topology of random 2-dimen-sional cubical complexes
Abstract. We study a natural model of random 2-dimensional cubical com-plex which is a subcom-plex of an n-dimensional cube, and where every possible square 2-face is included independently with probability p. Our main result is to exhibit a sharp threshold p= 1/2 for homology vanishing as n→ ∞. This is a 2-dim. analogue of the Burtin and Erdös–Spencer theorems characterizing the connectivity threshold for random cubical graphs. Our main result can also be seen as a cubical counterpart to the Linial–Meshulam theorem for random 2-dimensional simplicial complexes. However, the models exhibit strikingly different behaviors. We show that if p >1−√(1/2) ≈0.2929, then with high probability the fundamental group is a free group with one generator for every maximal 1-dimensional face.
Submitted, preprit arXiv:2001:07812

F. Manin, B. Schweinhart, É. Roldán
Topology and local geometry of the Eden model
Abstract. The Eden cell growth model is a simple discrete stochastic process which produces a "blob" in |R^d: start with one cube in the regular grid, and at each time step add a neighboring cube uniformly at random. This process has been used as a model for the growth of aggregations, tumors, and bacterial colonies and the healing of wounds, among other natural processes. Here, we study the topology and local geometry of the resulting structure, establishing asymptotic bounds for Betti numbers. Our main result is that the Betti numbers grow at a rate between the conjectured rate of growth of the site perimeter and the actual rate of growth of the site perimeter. We also present the results of computational experiments on finer aspects of the geometry and topology, such as persistent homology and the distribution of shapes of holes.
Submitted, preprint arXiv:2005.12349
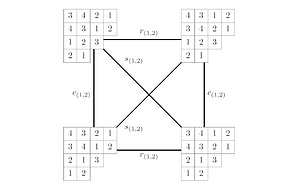
R. Karpman, É. Roldán
Isotopy graphs of Latin tableaux
Abstract. Latin tableaux are a generalization of Latin squares, which first appeared in the early 2000s in a paper of Chow, Fan, Goemans, and Vondrák. Here, we extend the notion of isotopy, a per-mutation group action, from Latin squares to Latin tableaux. We define isotopy graphs for Latin tableaux, which encode the structure of orbits under the isotopy action, and investigate the relation-ship between the shape of a Latin tableau and the structure of its isotopy graph. Our main result shows that for any positive integer d, there is a Latin tableau whose isotopy graph is a d-dimensional cube. We show that most isotopy graphs are triangle-free, and we give a characterization of all the Latin tableaux for which the isotopy graph contains a triangle. We also give a formula for the degree of a vertex of each component of an isotopy graph which depends on both the shape of the Latin tableaux and the filling.